How Polymers Behave in Dilute Solutions

Until now we have seen the factors by which the solubility of macromolecules is affected, from both physical, chemical and thermodynamic points of view. Now what happens to these macromolecules when they are dissolved?

Due to their large number of carbon atoms bonded together forming a long chain, polymers can generally adopt a lot of conformations. These conformations arise from the numerous internal rotations that can occur through simple C-C bonds, originating a number of rotational isomers.

Nevertheless, although the rotation of each bond is able to originate different conformations, due to energy restrictions not all of them have the same probability of occurrence. In such a case, the most stable conformations predominate in solution, like proteins and nucleic acids, that is in biopolymers mainly.

However, synthetic polymers particularly, can display a large number of possible conformations, and even though these conformations have not the same energy, the differences are small enough so that the chains can change from one conformation to another. This particularity gives a big flexibility to the macromolecules, and due to this flexibility, the chains do not adopt a linear form in solution, but a very characteristic conformation, known as random coil.

Figure 4. The random coil model

Such a flexibility can be understood more clearly with the help of molecular models, as shown in Figure 5.

Figure 5. A C-C simple-bonded chain and its spacial representation. (Redrawn from "Principles of Polymer Chemistry" / Paul J. Flory, Cornell University Press, Ithaca, 1953)

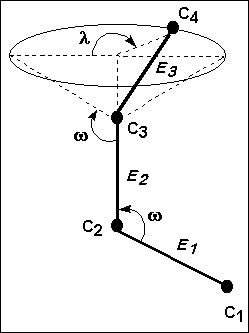
Let's assume C₁, C₂, and C₃ are carbon atoms in the same plane. According to this, the atom C₄ can occupy any place throughout the circle, which represents the base of a cone originated by the rotation of the bond E₃. The angles of such bonds are symbolized by w, whereas the location of atom C₄ is specified by the internal angle of rotation l.

For a macromolecule in the solid state, the angle l has a fixed value due to the restrictions of the network packing. That is why the possible rotational isomers do not occur. Nevertheless when this macromolecule is dissolved, the packing disappears and the angle l can vary widely, originating maximums and minimums of energy. Thus, the probability of reaching diverse stable conformations with each minimum of energy is high. On the other hand, the variation of the internal angle of rotation is associated to an energy change that, at minimums, is small. Hence, the chains can move freely to adopt such stable conformations. The fact that the chains are changing from one conformation to another is also favored, due to the low potential energy of the system. All these factors define, therefore, a flexible macromolecule and from these concepts, the typical random coil form arises.

You might ask if the "shape" or magnitude of the random coil would remain the same once the polymer has been dissolved. You will find that the answer is absolutely negative and that the situation will depend not only on the kind of solvent employed, but also on the temperature, and the molecular weight. The polymer-solvent interactions play an important role in this case, and its magnitude, from a thermodynamic point of view, will be given by the solvent quality. Thus, in a "good" solvent, that is to say that one whose solubility parameter is similar to that of the polymer, the attraction forces between chain segments are smaller than the polymer-solvent interactions; the random coil adopts then, an unfolded conformation. In a "poor" solvent, the polymer-solvent interactions are not favored, and therefore attraction forces between chains predominate, hence the random coil adopts a tight and contracted conformation.

In extremely "poor" solvents, polymer-solvent interactions are eliminated thoroughly, and the random coil remains so contracted that eventually precipitates. We say in this case, that the macromolecule is in the presence of a "non-solvent".

The particular behavior that a polymer displays in different solvents, allows the employ of a useful purification method, known as fractional precipitation. For a better understanding about how this process takes place, let�s imagine a polymer dissolved in a "good" solvent. If a non-solvent is added to this solution, the attractive forces between polymer segments will become higher than the polymer-solvent interactions. At some point, before precipitation, an equilibrium will be reached, in which DG = 0, and therefore DH = TDS, where DS reaches its minimum value. This point, where polymer-solvent and polymer-polymer interactions are of the same magnitude, is known as q state and depends on: the temperature, the polymer-solvent system (where DH is mainly affected) and the molecular weight of the polymer (where DS is mainly affected).

It may be inferred then, that lowering the temperature or the solvent quality, the separation of the polymer in decreasing molecular weight fractions is obtained. Any polymer can reach its q state, either choosing the appropriate solvent (named q solvent) at constant temperature or adjusting the temperature (named q temperature, or Flory temperature) in a given solvent. Table 2 compiles some values.

The q temperature is a parameter arisen from Flory-Krigbaum theory. It is used to calculate the free energy of mixing of a polymer solution in terms of the chemical potentials of the species. We will further study the q temperature relationship with other important parameters that characterize dissolved polymers.

So far we have analyzed the influence of the solvent and the temperature in the dimensions of the random coil. However is equally important to know what happens to the viscosity of the macromolecular solution as the solvent becomes poorer. Considering the chain molecules as rigid spheres, when a change from a "good" solvent to a "poor" solvent takes place, the spheres become contracted. According to the Einstein equation, the relative viscosity h_r is obtained from:

That is to say, dividing the viscosity of the solution (h) by the viscosity of the solvent (h_s). From equation [4] it can be noticed that h_s is directly proportional to the volume fraction f that these spheres occupy. Since, with the necessary considerations, this reasoning can be transferred to macromolecules, which are not rigid spheres, it may be inferred that if the segments are contracted in a "poor" solvent, the viscosity of the solution will be smaller. Therefore, viscosity can be adjusted according to the solvent quality.

Temperature, however, will not affect the viscosity of a polymer solution in a relatively "poor" solvent. In this case, it should be considered that as the temperature increases, the viscosity of the solvent (h_s) decreases. However, on the other hand, when the temperature is raised, a greater thermal energy will be granted to molecules. Consequently, these molecules will tend to expand themselves, increasing their volume fraction (f). Thus both effects are compensated, and for this reason the change of viscosity due to the increase of the temperature, is not significant.

The measurement of viscosity in dilute macromolecular solutions has a fundamental importance not only in the determination of molecular weights, but also, as we will discuss later, in the evaluation of key parameters for the understanding of the conformational characteristics of polymer solutions.

Copyright ©2005      Polymer Science Learning Center      Department of Polymer Science      The University of Southern Mississippi